Archive for the ‘Teknik Kompilasi’ Category
Teknik Kompilasi – Quiz 1 April
1. Perhatikan CFG (Context Free Grammar) berikut ini :
S -> S+A | S-A | A+S | A-S | B*A
B -> aB | B(a+B) | B*a | a(a+B) | b
A -> a
Tentukan First, Follow & Table dari Production data.
Jawab :
S -> ASˈˈ | B*ASˈ
Sˈ -> +ASˈ | -ASˈ | ԑ
Sˈˈ -> +SSˈ | -SSˈ
B -> aBˈˈ | bBˈ
Bˈ -> (a+B)Bˈ | aBˈ | ԑ
Bˈˈ -> BBˈ | (a+B)Bˈ
A -> a
First :
– First (S) = { a,b }
– First (Sˈ) = { +,-,ԑ }
– First (Sˈˈ) = { +,- }
– First (B) = { a,b }
– First (Bˈ) = { (,a,ԑ }
– First (Bˈˈ) = { a,b,c }
– First (A) = { a }
Follow :
– Follow (S) = { $ }
– Follow (Sˈ) = { $ }
– Follow (Sˈˈ) = { $ }
– Follow (B) = { *,),(,a }
– Follow (Bˈ) = { *,),(,a }
– Follow (Bˈˈ) = { *,),(,a }
– Follow (A) = { +,-,$ }
Tabel Produksi dari hasil diatas :
|
a |
b |
+ |
– |
( |
) |
* |
$ |
|
|
S |
S -> ASˈˈ |
S -> B*AS |
||||||
|
Sˈ |
Sˈ -> +ASˈ |
Sˈ -> ASˈ |
Sˈ -> ԑ |
|||||
|
Sˈˈ |
Sˈˈ -> +SSˈ |
Sˈˈ -> -SSˈ |
||||||
|
B |
B -> aBˈˈ |
B -> bBˈ |
||||||
|
Bˈ |
Bˈ -> aBˈ , Bˈ -> ԑ |
Bˈ -> (a+B)Bˈ , Bˈ -> ԑ |
Bˈ -> ԑ |
Bˈ -> ԑ |
||||
|
Bˈˈ |
Bˈˈ -> BBˈ |
Bˈˈ -> BBˈ |
Bˈˈ -> (a+B)Bˈ |
|||||
|
A |
A -> a |
2. S -> if E then S | if E then S else S | V := E
V -> id | id [E]
E -> E + T | E – T | T
T -> T * F | T / F | F
F -> V | (E) | const
Tentukan first, follow, dan tabel dari produksi tersebut.
Jawab
S -> if E then S’ | v := E
S’ -> ε | else S
V -> idV’
V’ -> ε | [E]
E -> TE’
E’ -> +TE’ | -TE’ | ε
T -> FT’
T’ -> *FT’ | /FT’ | ε
F -> V | (E) | const
- Menentukan first
first (S) = { id, if }
first (S’) = { ε, else }
first (V) = { id }
first (V’) = { ε, [ }
first (E) = { id, (, const }
first (E’) = { +, -, ε }
first (T) = { id, (, const }
first (T’) = { *, / , ε }
first (F) = { id, (, const }
- Menentukan follow
follow (S) = { $, else }
follow (S’) = { $, else }
follow (V) = { : }
follow (V’) = { : }
follow (E) = { ], ) }
follow (E’) = { ], ) }
fololw (T) = { +, -, ], ) }
follow (T’) = { +, -, ], ) }
follow (F) = { *, /, +, -, ] , ) }
Tabel Produksi dari hasil diatas :
|
|
id |
if |
else |
[ |
( |
const |
+ |
– |
* |
/ |
: |
) |
] |
$ |
|
S |
S->V:=E |
S->if E then S S’ |
|
|
|
|
|
|
|
|
|
|
|
|
|
S’ |
|
|
S’->else S
|
|
|
|
|
|
|
|
|
|
|
S’-> ε |
|
V |
V->idV’ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V’ |
|
|
|
V’->[E]
|
|
|
|
|
|
|
V’-> ε |
|
|
|
|
E |
E->TE’ |
|
|
|
E->TE’ |
E’->TE’ |
|
|
|
|
|
|
|
|
|
E’ |
|
|
|
|
|
|
E’->+TE’
|
E’->-TE’
|
|
|
E’-> ε |
E’-> ε |
|
|
|
T |
T->FT’ |
|
|
|
T->FT’ |
T->FT’ |
|
|
|
|
|
|
|
|
|
T’ |
|
|
|
|
|
|
T’-> ε |
T’-> ε |
T’-> *FT’ |
T’-> /FT’ |
|
T’-> ε |
T’-> ε |
|
|
F |
F->V |
|
|
|
F->(E) |
F->const |
|
|
|
|
|
|
|
|
3. S -> a= A
A -> aA’|bA’
A’ -> + AA’ | ԑ
Carilah First dan Follow serta buatlah tabel produksinya!
First (S) = {a}
First (A) = {a,b}
First (A’) = {+, ԑ}
Follow (S) = {$} menggunakan syarat algoritma follow 1
Follow (A) = {$, +} menggunakan syarat algoritma follow 2 dan 3a
Follow (A’) = {$, +} menggunakan syarat algoritma follow 2
Sehingga tabel produksinya adalah
|
|
a |
b |
+ |
$ |
|
S |
S -> a=A |
|
|
|
|
A |
A -> aA’ |
A ->bA’ |
|
|
|
A’ |
|
|
A’ -> +AA’ , A’-> ԑ |
A’ -> ԑ |
4. be -> bt be’
be’ -> or bt be’
be’ -> ԑ
bt -> bf bt’
bt’ -> and bf bt’
bt’ -> ԑ
bf -> not bf
bf -> (be)
bf -> true
bf -> false
Cek string sbb: not (true or false) and true and true and false not (false) true
|
No |
Stack |
Input |
Output |
|
1 |
be$ |
not (true or false) and true and true and false not (false) true$ |
be -> bt be’ |
|
2 |
bt be’$ |
not (true or false) and true and true and false not (false) true$ |
bt -> bf bt’ |
|
3 |
bf bt’ be’$ |
not (true or false) and true and true and false not (false) true$ |
bf -> not bf |
|
4 |
not bf bt’ be’$ |
not (true or false) and true and true and false not (false) true$ |
Pop not |
|
5 |
bf bt’ be’$ |
(true or false) and true and true and false not (false) true$ |
bf -> (be) |
|
6 |
(be) bt’ be’$ |
(true or false) and true and true and false not (false) true$ |
Pop ( |
|
7 |
be) bt’ be’$ |
true or false) and true and true and false not (false) true$ |
be -> bt be’ |
|
8 |
bt be’ ) bt’ be’$ |
true or false) and true and true and false not (false) true$ |
bt -> bf bt’ |
|
9 |
bf bt’ be’ ) bt’ be’$ |
true or false) and true and true and false not (false) true$ |
bf -> true |
|
10 |
true bt’ be’ ) bt’ be’$ |
true or false) and true and true and false not (false) true$ |
Pop true |
|
11 |
bt’ be’ ) bt’ be’$ |
or false) and true and true and false not (false) true$ |
bt’ -> ԑ |
|
12 |
be’ ) bt’ be’$ |
or false) and true and true and false not (false) true$ |
be’ -> or bt be’ |
|
13 |
or bt be’ ) bt’ be’$ |
or false) and true and true and false not (false) true$ |
Pop or |
|
14 |
bt be’ ) bt’ be’$ |
false) and true and true and false not (false) true$ |
bt -> bf bt’ |
|
15 |
bf bt’ be’ ) bt’ be’$ |
false) and true and true and false not (false) true$ |
bf -> false |
|
16 |
false bt’ be’ ) bt’ be’$ |
false) and true and true and false not (false) true$ |
Pop false |
|
17 |
bt’ be’ ) bt’ be’$ |
) and true and true and false not (false) true$ |
bt’ -> ԑ |
|
18 |
be’ ) bt’ be’$ |
) and true and true and false not (false) true$ |
be’ -> ԑ |
|
19 |
) bt’ be’$ |
) and true and true and false not (false) true$ |
Pop ) |
|
20 |
bt’ be’$ |
and true and true and false not (false) true$ |
bt’ -> and bf bt’ |
|
21 |
and bf bt’ be’$ |
and true and true and false not (false) true$ |
Pop and |
|
22 |
bf bt’ be’$ |
true and true and false not (false) true$ |
bf -> true |
|
23 |
true bt’ be’$ |
true and true and false not (false) true$ |
Pop true |
|
24 |
bt’ be’$ |
and true and false not (false) true$ |
bt’ -> and bf bt’ |
|
25 |
and bf bt’ be’$ |
and true and false not (false) true$ |
Pop and |
|
26 |
bf bt’ be’$ |
true and false not (false) true$ |
bf -> true |
|
27 |
true bt’ be’$ |
true and false not (false) true$ |
Pop true |
|
28 |
bt’ be’$ |
and false not (false) true$ |
bt’ -> and bf bt’ |
|
29 |
and bf bt’ be’$ |
and false not (false) true$ |
Pop and |
|
30 |
bf bt’ be’$ |
false not (false) true$ |
bf -> false |
|
31 |
false bt’ be’$ |
false not (false) true$ |
Pop false |
|
32 |
bt’ be’$ |
not (false) true$ |
Rejected |
Teknik Kompilasi TM 1
Soal :
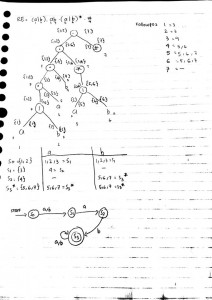
Buatlah Soal RE dan konversikan ke DFA dengan ketentuan sebagai berikut :
- Jumlah State DFA min 5 dan max 8.
- Jumlah Final State DFA min 2 dan max 3.
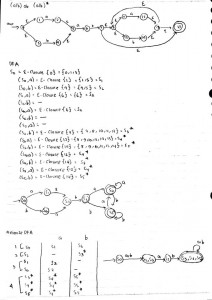
Tentukan : RE, ε-NFA, DFA, dan Min DFA
———————————————————————————————————–
Jawaban :
Melalui cara follow post ternyata langsung didapat DFA minimizednya :